原文地址：面积比原理在潜水泵设计中的应用研究

　　潜水泵是应用最广泛的通用机械,不仅用于工业,还用于广大农村。随着农村电气化的发展,从生活用水到农田灌溉,潜水泵已成为必不可少的工具。它的使用量大面广,为了扩大使用范围,本文提出一种基于面积比原理的水泵设计方法。潜水泵的性能主要是由叶轮和导流器两方面决定的,高效率的泵不但要求高效的叶轮,而且还需要与叶轮良好匹配的导流器,如果导流器不适配,不仅降低泵的效率,而且还会在一定程度上影响泵性能的稳定 。H H Anderson提出了离心泵的面积比原理,指出叶轮出口过流面积与泵体喉部面积之比是泵扬程、流量、轴功率等参数的主要决定因素。R CWorster首次用数学方法证明了H H Anderson所提出的面积比原理的科学性 。

　　我国从20世纪80年代初开始引进面积比原理也曾有人运用面积比原理对现有泵进行分析,但研究工作还不够深入,为此,本文提出一种基于面积比原理的水泵设计方法,即在保持面积比系数不变的条件下,对同一导流器选配不同的叶轮以获得不同参数的高效水泵。并通过试验研究和数值模拟对该方法进行验证。

1、面积比原理的理论

　　在水泵叶轮设计中,一般假设叶轮进口无预旋,即v_u,1=0,则水泵的基本方程式为:

式中H_T ———泵的理论扬程, m
　　u₂ ———叶轮出口圆周速度, m/s
　　v _{u, 2} ———叶轮出口水流绝对速度的圆周分量, m/s

　　根据叶轮出口速度三角形可知:

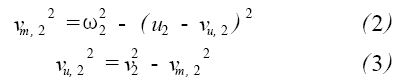
　　假设叶轮出口到导流器的喉部这一过渡区无任何水力损失, 则有v₂ = v_t , 将式(2)代入式(3)得:

　　叶轮将能量传递给液体, 导流器收集从叶轮流出的液体并将液体导出。导流器对液体不增加任何的能量,但影响泵的运行工况点和最高效率点。叶轮与导流器的耦合应遵守液体流动的连续性方程,则有:

式中v _t ———导流器喉部水流速度, m/s
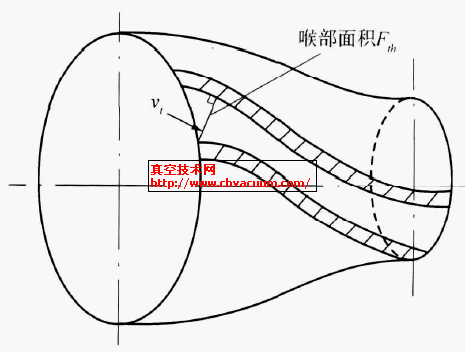
　　F_th ———导流器喉部面积, mm²
　　ω₂ ———叶轮出口叶片间的相对速度, m/s
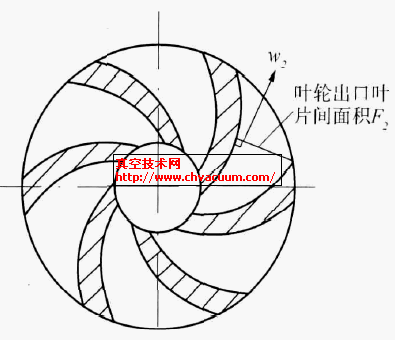
　　F₂ ———叶轮出口叶片间面积, mm²

　　将式(5)改写为:

　　式中Y———面积比系数

　　将式(4)、(6)代入式(1) ,得泵的理论扬程与面积比系数的关系式为:

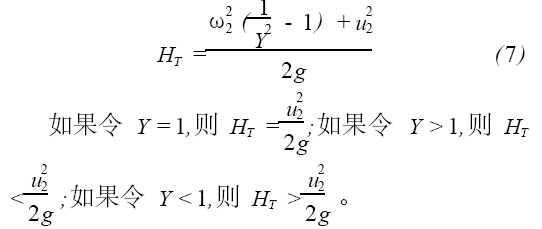
　　可见,要获得较高的水泵扬程,应使面积比系数Y≤1。

　　张俊达对166种泵的水力模型面积比系数进行了统计和回归,并绘制出了面积比系数与泵比转数的关系曲线,得出绝大部分泵的面积比系数Y≤1,进一步证明了上述研究结论是正确的。郭自杰推导出了面积比系数与比转数的近似表达式,并对大量离心泵的面积比系数进行了统计,数据表明它们的面积比系数Y≤1。据此,本文提出了在保持面积比系数不变的条件下,对同一导流器通过选配叶轮来获得高效水泵。

2、测试装置与试验研究

　　为了研究面积比系数对潜水泵性能的影响,用井用潜水泵做试验。对同一导流器分别选配2种叶轮,在兰州理工大学开式试验台上进行测试,试验时电动机不变只更换泵。为了保证吸入区不发生气蚀和漩涡,叶轮在水下有足够的淹没深度。电动机的输入功率采用电测法测定,电动机效率按铭牌上的效率估算。取250QJ125型潜水泵进行试验,在保持导流器喉部面积与叶轮出口叶片间的面积之比即面积比系数Y=0.87不变的前提下,重新设计一个叶轮Ⅱ,将此叶轮装在该潜水泵的导流器上进行试验。选配2种不同叶轮的潜水泵,它们各自的最佳工况点实测数据如表1所示。

表1　最佳工况点实测值

 

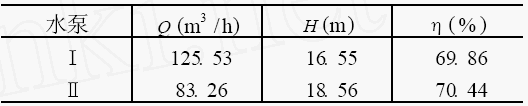
图1　叶轮出口叶片间面积示意图2　导流器喉部面积示意

表2　叶轮出口叶片间面积和导流器喉部

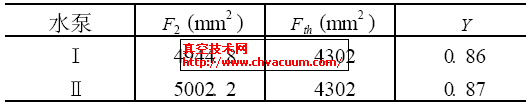
　　为了确保试验数据的可靠性,作者对叶轮出口叶片间的面积和导流器喉部面积进行了实测。图1、2为叶轮出口叶片间面积和导流器喉部面积的确定方法,表2为实测结果。从表2中可以看出:两个水泵面积比系数稍有偏差,这是由零件加工误差造成的。在导流器不变的情况下选配不同叶轮,只要保持面积比系数不变,完全可以得到一种高效率的潜水泵。

3、潜水泵内部流场的三维湍流数值模拟

3.1、计算方法及计算区域

　　采用FLUENT数值计算软件,对潜水泵内的三维不可压缩定常湍流流动进行数值计算。选用分离式求解器、采用非结构化交错网格的SIM-PLEC算法及隐式求解。采用有限体积法离散计算区域,动量方程、湍动能、耗散率均采用一阶迎风格式离散,一阶迎风格式所生成的离散方程的截差等级较低,限制了解的精度,但采用该离散格式计算一般不会出现解的振荡。

　　运用AutoCAD对潜水泵进行三维实体造型。为了使叶轮前后盖板带动旋转的液体能够顺畅地流入压水室,回收一部分圆盘摩擦功率,提高泵的效率,同时也为能更准确地描述潜水泵中的速度、压力等参数的变化规律,在叶轮的进口边添加一段高为60mm的同心圆柱体,与此同时,在导流器出口边亦添加一段高为60mm的同心圆柱体,使出流液体能够得到充分发展。图3～5为潜水泵实体造型。

图3　整体模型图Ⅰ图4　整体模型图Ⅱ

图5　FLUENT计算模型

　　以潜水泵单级泵壳内流道为计算区域,采取全流道模拟方式,同时将整个计算区域划分为4个部分,即泵的进口延伸段、叶轮室的旋转部分、导流器区域的静止部分和出口延伸段。两个子区域之间连接的平面作为分界面。对于旋转部分和静止部分之间的耦合采用多参考系模型。由于叶轮、导流器叶片形状复杂,扭曲严重,为使计算网格更好地描述模型的结构特征,尽量做到不失真,故采用对复杂边界适应性强的混合网格。同时,对叶轮、导流器叶片表面进行网格细化。图6为潜水泵计算网格模型。

图6　潜水泵计算网格模型

3.2、控制方程及边界条件

　　控制方程采用三维雷诺时均N-S方程,选用RNG湍流模型组成的封闭方程组。近壁处理采用固壁无滑移假设,并应用标准壁面函数处理。模型常数为: k=0.039,ε=0.19, Cμ=0.0845, C1=1.42, C2=1.68。

　　流动的液体为水, 液体密度取ρ=998. 2kg/m³ ,水的动力粘度为μ=1. 0 ×10^-3 N·s/m²。进口边界条件为垂直于进口的平均流速V, V =Q/A_进口=4Q/πd² = 5. 226m/s; 出口边界条件为自由出流。

3.3、计算结果及分析

　　同一导流器选配2种不同叶轮的潜水泵最佳工况点模拟数据如表3所示。

表3　潜水泵最佳工况点模拟数据

　　潜水泵最佳工况点的数值模拟结果与试验实测结果较为吻合,误差很小。误差产生的原因有:

　　(1)建模时忽略了叶轮与导流器之间间隙对泵性能的影响;

　　(2) FLUENT软件模型误差,如RNG k -ε湍流模型与实际的湍流流动并不一定完全符合,湍流模型是在一定的条件下对实际问题的近似处理。同时,离散误差、舍入误差也会对计算结果造成影响;

　　(3)计算边界条件、网格划分及对实际问题的简化处理也是产生误差的原因;

　　(4)水力效率、容积效率和扬程修正系数的估算正确性。

4、结论

　　(1)叶轮出口叶片间的过流面积和导流器喉部面积是控制潜水泵性能的重要因素,满足面积比系数Y≤1,就可获得较高的水泵扬程;

　　(2)通过试验研究,在面积比系数不变的前提下,导流器不变只改变叶轮同样可以得到一种高效率的潜水泵;

　　(3)数值模拟计算结果和试验实测结果较为吻合,运用CFD数值模拟方法来预测潜水泵性能是完全可行的;

　　(4)本试验仅对一种潜水泵进行了试验分析,并且数量有限,有待于进一步深入研究。