沉淀池和澄清池是净水工艺中的重要处理单元,其主要作用是促进固液分离,降低后续处理单元的固体负荷。固液分离效果与单元内的水力停留时间、进出口布置形式及排泥效果等因素有关[1, 2]。穿孔花墙和格栅等均匀进水口布置形式旨在使整座沉淀池或澄清池的平面负荷一致,而出口的均匀集水对于不发生池内短流及保证出流水质一致至关重要[3, 4, 5]。在实际运行中风力形成水面坡降、池子不均匀沉降和出水口安装高度不一致等因素往往导致局部出流量较大[6],扰动带起沉淀物,影响沉淀效果,降低出水水质[7]。
沉淀池和澄清池出水堰的合理设计和布置对保证沉淀效果非常重要[8, 9]。三角堰是目前沉淀池和澄清池主要采用的集水出流构造。风波动、不均匀沉降和安装误差等因素使得堰上不同位置的液位高度不一致,较高液位在较大出流断面下出流量大,较低液位在较小出流断面下出流量小,导致辐流式和竖流式等圆形沉淀(澄清)池圆周负荷不同,平流沉淀池和斜板沉淀池等矩形沉淀池出流段平面负荷不同,短流降低了出流池子的出流水质。此外,随着水质标准的提高,对沉淀处理效果的要求也逐步提高,对沉后水给出了明确的规定,因此适当的工艺改造对改善沉淀池的沉淀效果及提高处理能力十分必要[10]。
笔者通过降低堰上高液位处出流断面面积来缩小高低液位差之间的流量,提出了一种新型的可在堰上水面变化时使出水更为均匀的菱形堰,确定了菱形堰出流流量与堰上水位之间的关系,验证了菱形堰相对于目前常用的三角堰在集水方面的优越性及可行性。
1 三角堰的发展及问题分析
最初理想沉淀池的出水堰只是在池末端简单设置平板[11],但在实际安装和运行中发现总是不能保证平板堰的完全水平,且易受风力形成水面坡降、池子不均匀沉降等因素影响,导致短流现象的出现,使得整个池子的出流水质不一致。为保证出水的均匀性,发展出了三角出流堰。平板堰与三角堰的出流效果对比见图1(a)。
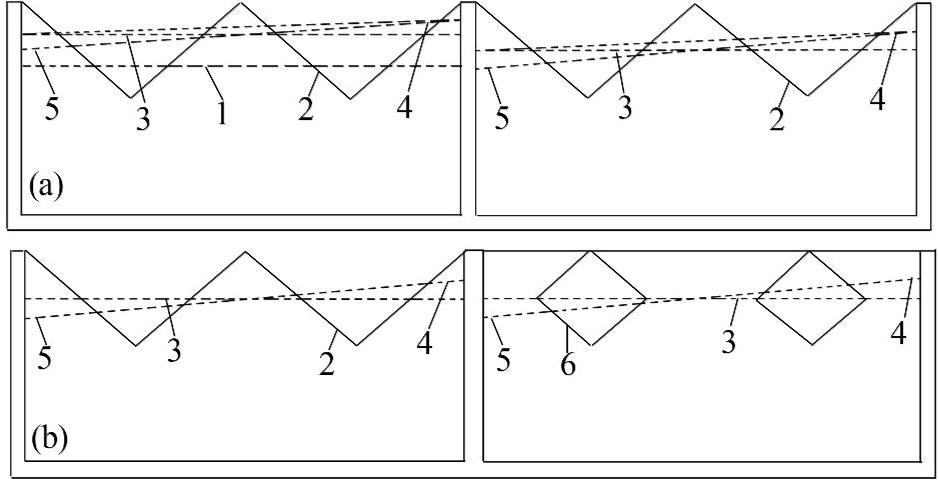
1—平板堰;2—三角堰;3—设计水位; 4—高水位处;5—低水位处;6—菱形堰。
图1 三角堰与平板堰、菱形堰的对比
假设平板堰和三角堰的出水流量相等,在风波动、不均匀沉降和安装误差等因素影响下,平板堰和三角堰的各位置上的液位高度不一致,较低液位处在较小出流断面下的出流量较小,较高液位处在较大出流断面下的出流量较大,但由于三角堰较高液位处的出水断面小于平板堰较高液位处的出水断面,可以缩小高低液位之间的流量差,从而达到均匀出水的目的。因此三角堰被广泛应用,其中以直角三角堰最为普遍。
但在实际运行中发现,三角出水堰受风力等影响时,较高液位处的流量还会明显增加,而较低液位处的流量仍明显减小,依然会造成短流现象,且使得底层沉积物向上迁移,影响悬浮物的正常沉降,不能保证更好、更稳定的出水效果。随着沉淀池的不断发展,出现了辐流式和竖流式等圆形沉淀池,这些沉淀池的集水出流构造也普遍采用三角堰,运行中发现辐流式和竖流式等圆形沉淀池的出水也存在上述问题。为得到更好的出水水质,延续了三角堰的降低堰上高液位处出流断面面积以缩小高低液位之间流量差的理念,提出在堰上水位变化时能保证更均匀出水的菱形堰,进一步缩小高液位时的出流断面面积,见图1(b)。
2 菱形堰的提出
菱形堰是基于降低堰上高液位处出流断面面积以缩小高低液位差之间流量提出的,它可以减小受风力等因素影响时高液位处的出流量,从而使整个构筑物的出水更加均匀、一致。
受风力因素影响时,低液位处的出流量会减少,高液位处的出流量会增加。以图2进行说明,在设计水位正常运行的构筑物受到风的影响时,三角堰低水位一侧的水位下降了a高度,其流量为Q1降,高水位一侧的水位升高了a高度,流量为Q1升;菱形堰的水位分别下降和上升了a高度,流量分别为Q2降、Q2升。由图2可以看出Q1降=Q2降、Q1升>Q2升,两流量的差值如图2阴影部分所示,这样在理论上说明了菱形堰可以减缓构筑物一侧出水流量的增加,达到整体出水均匀的目的。
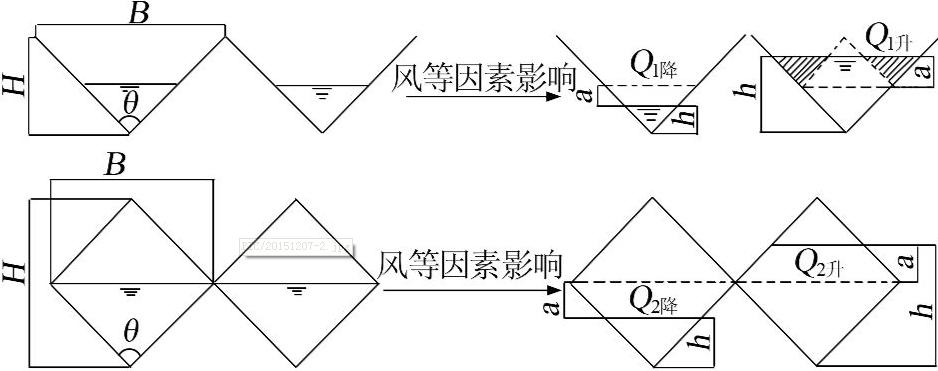
图2 菱形堰与三角堰理论说明示意
菱形堰出流非完全自由式水面,不能采用自由式堰流公式计算。需经实验确定菱形堰出流量与堰上水位的关系,通过拟合方式获得菱形堰堰流公式。鉴于目前沉淀池常采用的三角堰的H和B分别为80、160 mm,实验中菱形堰的H和B均为80 mm。
3 菱形堰流量公式的确定
3.1 实验装置
实验装置如图3所示。
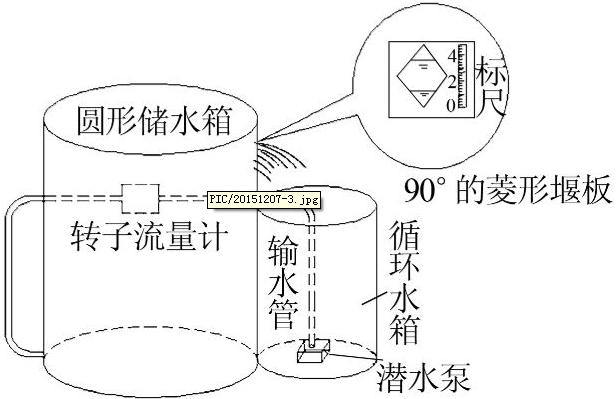
图3 实验装置
包括圆形储水箱(直径1.7 m,高2.2 m),其上部安装了堰角为90°的菱形堰板(80 mm),在外设置循环水箱(直径0.5 m,高1.6 m)和潜水泵,通过调整潜水泵流量确保储水箱水位恒定,由转子流量计计量圆形储水箱的进出流量。
3.2 实验条件
实验在圆形储水箱上安装90°的菱形堰板,由潜水泵将循环水箱内的水打入圆形储水池内,通过调节流量使水位上升至菱形堰某一水位,在堰上和桶后观察窗处记录前后水头(选取前后水头连线上最接近理论值的一点作为最终水头),圆形储水箱内的水通过菱形堰后再次流入循环水箱内形成环路。实验设计的菱形堰堰高(H)为80 mm,流量变化范围为80~5 000 L/h,水头变化范围为10~70 mm。
3.3 结果与讨论
(1)实验可靠性的验证。菱形堰的对角线以下(h<H/2)仍可以看成是1个直角三角堰,因此理论上应符合直角三角堰的流量计算公式,见式(1)。
![]()
式中:μ——流量系数,一般取0.6;
h——水头,m[12]。
对90°堰角的h<H/2时的实测流量与理论流量进行对比,如图4所示。
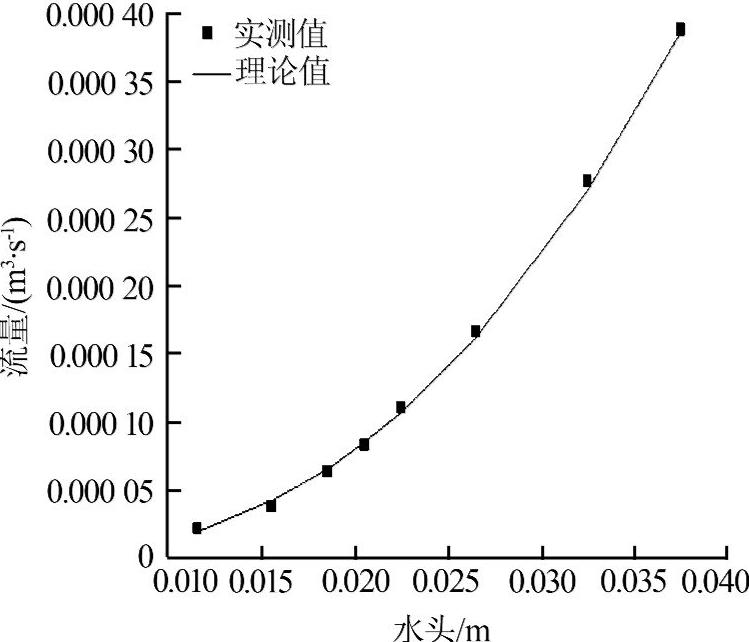
图4 h<H/2时菱形堰流量(堰角90°)的实测值与理论值
从图4可以看出,理论流量与实测流量基本重合。使用皮尔逊相关系数法计算得到实测流量与理论流量的相关系数为0.999 7,接近于1,验证了此次实验的可靠性。
(2)菱形堰h>H/2时的流量公式拟合。为验证菱形堰的出水均匀性,需通过实验得到菱形堰的流量公式。当h>H/2时,流量计算不能采用一般的堰流公式,而采用直接拟合方式得到该实验条件下的流量公式。实验结果如图5所示,经过多次拟合得到菱形堰流量公式,见式(2)。
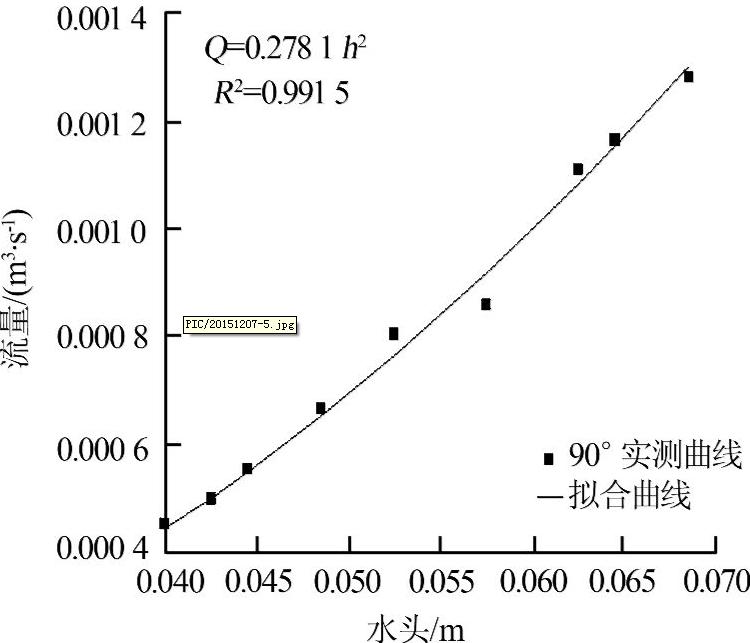
图5 h>H/2时菱形堰(堰角90°)的流量公式拟合
4 菱形堰与三角堰的出流均匀性对比
由上述实验结果可知,菱形堰的流量公式为
![]()
(2)h>H/2时,Q=0.278 1 h2时,Q=0.278 1 h2。对风力影响下2种出水堰的流量进行对比,结果如表1所示。
沉淀(澄清)池在不受任何条件影响正常出水时,其各个位置的出流量是一致的,因此各处出流量之间的比值都应为1。如表1所示,在风等因素影响下,随着水位升高和降低a值的不断增大,三角堰和菱形堰的Q升不断增大,Q降不断减小,其中菱形堰的Q2降/Q2升为0.91,较Q1降/Q1升(0.88)更接近于1。
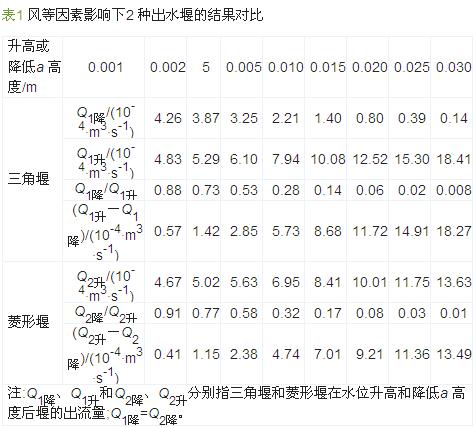
随着a的增大,Q2降/Q2升越来越偏离1,但由Q升-Q降可知,随着a不断增大,三角堰的Q1升-Q1降由0.57增加到18.27,菱形堰的Q2升-Q2降由0.41增加到13.49,比较后可知,菱形堰随着a的增加其较低水位与较高水位之间的流量增加趋势较三角堰缓慢,且菱形堰的较高水位与较低水位之间的流量都小于三角堰较高水位与较低水位之间的流量。因此说明降低堰上高液位处出流断面面积可以缩小高低液位之间的流量差,从而使堰上水面发生变化时出水更为均匀,即菱形堰较三角堰出水更加均匀。
对比了2种出水堰水位升高处与降低处的流量差,如图6所示。

图6 2种出水堰水位升高处与降低处的流量差
由图6可见,a由0.005增加到0.030时,2种出水堰的Q升-Q降也不断增加,虽然二者的水位增加间隔都是0.005 m,但随着a的增加2个出水堰的Q升-Q降差距越来越大,说明a越大,菱形堰的出水均匀性越明显,也就是说风等因素对沉淀(澄清)池影响越大,菱形堰对保障出水均匀性的作用越大。
5 结论
(1)对菱形堰h<H/2时的实验流量与水头关系、三角堰理论流量与水头关系进行对比分析,验证了实验的可靠性。
(2)分析了菱形堰(堰角90°)的流量与水头的对应关系,得出实验条件下菱形堰的流量公式,并验证了菱形堰的出水均匀性比三角堰的出水均匀性更好。
