EXCEL在风险管理模拟中的应用*

熊义杰

（西安理工大学 经济与管理学院 710054）

 

1. 什么是模拟

模拟(Simulation)也叫做系统仿真，是一种通过物理、逻辑或数学模型进行数据试验的技术，它通过真实事物的模型，进行反复的数据试验，以获取供决策使用的有关信息。一个完整的模拟模型总是少不了要包括两个部分的内容，即逻辑表达式和数学表达式。逻辑表达式告诉我们在给定输入的条件下如何得出输出值。任何模拟模型必然包括两种输入，即可控输入（也叫确定性输入）和概率输入（也叫随机性输入）。图1给出了模拟模型的逻辑表达式（也叫概念模型）。从方法论的角度看，模拟主要是和随机变量的概率分布打交道，并把它们组合起来供决策使用。模拟分析方法适用于大量包含有随机现象和动态过程的概率型决策问题。

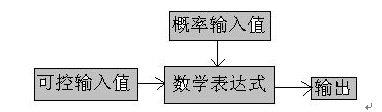
图1 模拟模型的逻辑表达式

    比如，企业在确定生产某一种新产品时，通常要先考虑它的价格、质量、销售、竞争力和市场情况等；商场在确定收银台财务人员的编制时，需要考虑每日顾客数量的变化、财务人员的工作能力和水平，以及临时售货的特殊需要等等。所有这些问题均包含有大量随机事件、许多相互关联的变量以及随着时间而变化的动态过程，往往很难找到现成的方程式或最优化模型加以解决。

模拟方法的提出和发展，与现代计算机科学的发展密切相关。然而这一方法建立的思路，却与一位法国科学家在200多年前提出的一个问题即蒲丰（Buffon）投针问题(1777)密切相关。问题是这样的：在平面上画一些平行线，相互间的距离都等于a，向此平面任投一长度为l 的针（ l <a）,问针与任一平行线相交的概率是多少。

    设以x表示针的中点到最近一条平行线的距离，φ表示针与平行线的交角，针与平行线的位置如图2所示，显然只有在条件： 0≤x≤a/2，0≤φ≤π，x≤(l/2)sinφ    满足时，针才与平行线相交。所以，相交的概率应该是：

 

 

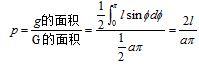
由于最后的答案与π有关，所以不少人曾经利用它来计算π的数值。方法是记下投针的次数N和相交的次数n，再代入下面的公式中计算π：

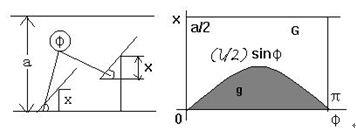
         图2 蒲丰（Buffon）投针问题

 

表1是投针试验的一些历史资料。

       表1         历史上的投针试验结果

    

 

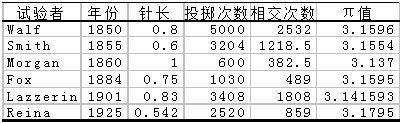蒲丰问题给我们的重要启示是：可以建立一个概率模型，它与我们感兴趣的亮有关（如其中的π），然后设计适当地随机试验，并通过这一试验的结果来确定这一量值（如上述的π）。现在，随着现代电子计算机的发展，人们已经按照这一思路建立了一种全新的方法，即蒙特卡罗方法（Monte-Carlo Method），也就是模拟方法或系统仿真方法。

    蒲丰投针问题在计算机上很容易实现[1]。

2．模拟方法的应用

我们来一起看一个案例。

   某公司拟引进一新产品生产技术，已知固定费用为10000元，考虑到竞争情况，产品价格只能定为2元/个。由于单位变动成本和需求量尚不确定，故只能估计确定。据乐观估计，单位变动成本可能在0.95~1.05元之间；而需求量则与竞争情况有关。当竞争强烈时，年销售量估计有8000、9000或10000个三种可能；当竞争不很强烈时，年销售量估计也是三种可能，即分别为10000、11000或12000个。估计竞争强烈的可能性为60％。试分析该公司是否该引进此新产品生产技术？

    在这里分析的难度是变动成本和需求量不确定，如果这两个指标确定，则利用下述的公式将不难进行决策（只要盈利就应认为是合算的）：

             盈亏值＝（单价－变动成本）×需求量－固定成本

现在运用模拟方法来进行分析。这里有三个随机变量，假定它们都是均匀分布的，于是可采用随机抽样（或抓阄）的方法来确定变量的对应关系。单位变动成本可以用A～J的某一花色扑克牌代表0.95~1.05这11个数（假定变量离散），另取A～10的另一花色扑克牌代表竞争状况（前6个点代表强），再各用三张扑克分别代表相应竞争状况下的三种销售量，将这些扑克牌分别放入4个罐中，采用有放回抽样。每抽样一次，可利用上式求出一个盈亏值。在大量抽样的条件下，则可求出一个盈利概率，这将为决策提供有用的参考信息。

该模拟问题的逻辑表达式如图3所示。

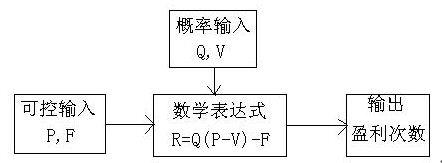
                 图3 产品开发问题的逻辑表达式

上述的问题用计算机模拟并不复杂。对上述数据模拟，持平以上效果的概率稳定在45％左右。显然，可行性比较差。但如果给强烈竞争条件下的三个销售量均增加1000单位，则持平以上概率可达到65％[2]。这个结果应该说是比较理想的。

    由以上不难看出，模拟实际上是一种取样方法，它分析的结果只能产生统计估计，而不能提供最优解。由于模型中包含有随机变量，所以每一次试验结果都具有偶然性。因此，在模拟分析中，必须进行大量重复试验。每一次的试验结果只是一个样本，大量的试验结果才具有统计意义。

    模拟分析在经济管理中有着非常重要的实际应用价值。除了前面讲到的以外，后面几章中要学习的库存论、排对论问题都可以通过模拟分析来研究。模拟分析应用的一般步骤是：

（1）明确目标。模拟方法的目的，主要是帮助了解一个已有的系统，或者设计一个新系统。目标决定着变量的取舍。

（2）建立模型。即使用明确的数学或逻辑语言，确定系统应包括的变量，变量的性质及相互之间的关系。对模型的基本要求是可靠、有效，但又不过分复杂。可靠是指在同样的条件下进行试验，应能得到相同的结果。有效是说模型应能够反映真实的客观事物。最后，就是要考虑简明性。

（3）确定各变量的分布形式。模拟方法的一个重要步骤或关键技术，就是根据已有的资料和情报信息，对每个随机变量的分布即它们各自可能的取值范围及其概率，进行估计。这可以利用统计法（或频数法）、主观判断法和理论概率分布法等方法进行。其中，理论概率分布常用的如均匀分布、三角分布、正态分布、对数正态分布、负指数分布和爱尔朗分布等等，在模拟分析中都会经常用到。

（4）试验设计及其结果评价。在试验过程中，必须认真地做好记录、观察和数据分析。最后，要根据统计结果作出概率分布和统计图。

模拟分析的成功，有赖于对所研究对象或系统的清楚和透彻的了解。

3．模拟方法在Excel上的实现

在EXCEL上进行模拟，经常需要用到以下两个函数：

    1. RAND( )：即生成一个0和1之间的随机数；

    2. IF (逻辑判断，值1（真时），值2（不真时） )：这实际上是一个条件赋值函数，括号中需先给出一个逻辑判断式，比如b1>=5，当判断为真时，给值1，判断不真时，给值2。需注意的是，函数 IF 最多可以嵌套七层。

上述案例在Excel上模拟的步骤是：

第一步，先生成单位变动成本随机数，因为单位变动成本有11个数，所以可在B3单元格输“=11*RAND() ”即可；

    第二步，根据生成的随机数，给单位变动成本赋值，所以可在C3单元格输“=IF(B3>=10,1.05,IF(B3>=8.5,1.04,IF(B3>=7,1.025,IF(B3>=5.5,1.01,IF(B3>=4,0.995,IF(B3>=2.5,0.98,IF(B3>=1,0.965,0.95)))))))”即可；

第三步，生成市场竞争强弱随机数，可在D3单元格输“=10*RAND() ”即可。

    第四步，生成需求量随机数，可在E3单元格输“=30* RAND( ) ”即可。

    第五步，根据生成的随机数，给年销售量赋值，所以可在F3单元格输“=IF(D3>=4,IF(E3>=20,8000,IF(E3>=10, 9000,10000)),IF(E3>=20,10000,IF(E3>=10,11000,12000)))”

    第六步，计算盈亏值，可在G3单元格输“=(2-B3)*E3-10000”即可。

    第七步，统计盈利次数，可在H3单元格输“=IF(G3>0,H2+ 1, H2)”即可(因为累计需要一个初值，所以需先在H2输0)。

第八步，计算盈利次数百分比，可在I3单元格输“=H3/A3”即可（A3是序号，也是试验次数）。

下面可以再看一个实例。

假定有一个渔夫捕到了很多鱼，现在需要对卖鱼的市场进行决策 ,情况是这样：每天捕鱼的成本定为10000元 ,捕鱼量定为 3500公斤 ,假定可在两独立市场Ａ和Ｂ之一出售。市场Ａ很大 ,鱼价稳定在每公斤3.25元 ,且鱼可全部销售；市场Ｂ较小，但鱼的价格较高 ,服从均值为3.65、标准差为0.2的正态分布 ,但有鱼卖不出的风险 ,鱼的需求服从如下离散概率分布：

需求量	0	1000	2000	3000	4000	5000	6000
概  率	0.02	0.03	0.05	0.08	0.33	0.29	0.20
累积概率	0.02	0.05	0.10	0.18	0.51	0.80	1.00

现在的问题是：渔夫应该选择在市场Ａ ,还是市场Ｂ销售 ?市场Ｂ比市场Ａ的收入多的概率有多大 ?市场Ｂ收入的概率分布的形状如何 ?

根据已知条件，市场Ａ的收入是一个确定的量：3.25×3500 - 10000 =1375元；

市场Ｂ的收入是随机变量Ｒ=Ｐ×Min(3500,Ｄ)- 10000 ,其中 ,Ｐ和Ｄ分别是市场Ｂ的鱼价和鱼需求量 ,分别服从如上的正态分布和离散概率分布。

该问题的困难是你不可能去捕 100次鱼 ,得到100个统计数据来分析上述问题 ,模型模拟为我们解决了大问题。模拟的关键在于正态分布和离散分布的生成 ,这可以利用Excel的随机数生成函数rand()。下简要给出操作步骤。

第一步：先生成市场Ｂ对鱼需求量的离散分布。在工作表的A1单元格输入“=RAND()”；在B1单元格输入“=IF(A1<=0.02,0，IF(A1<=0.05,1000，IF(A1<=0.10,2000，IF(A1<=0.8,3000，IF(A1<=0.51,4000,IF(A1<=0.80,5000,6000))))))”；在单元格C1输入“=MIN(B1,3500)”。

第二步 : 生成市场Ｂ鱼价的正态分布。在单元格D1输入“=RAND()”；在E1输入“=NORMINV(D1,3.65,0.2)”。函数NORMINV(D1,3.65,0.2)的意义是生成一个均值为3.65,标准误差为0.2的正态变量。

第三步：求在Ｂ市场可取得的销售收入。在单元格F1输入“=E1*C1-10000”,即为在Ｂ市场售鱼的收入。

第四步 :将第一行向下复制100 (拖放),得到 100个售鱼的样本数据。然后，可以利用COUNTIF()函数估出利润大于1375的样本数目。对于此例，可在G1单元格输入“=COUNTIF($G$3:G3,">=1375")”即可，其中，$G$3表示绝对引用，在拖放过程中值不变。也可以使用累计函数（=IF(G3>=1375,H2+1,H2)）。经多次模拟试验（改变A、D和E列的值, 将光标置于工作表中的任一空白单元格中并按回车键一次可实现），利润大于等于1375的样本数稳定在80左右。毫无疑问，应选择B市场。