马尔科夫过程在管理预测中的应用*

熊义杰

（西安理工大学 经济与管理学院 710054）

摘要

马尔科夫过程就是把一个随机过程看作是一系列状态不断转移的过程。其基本原理是，在某一动态系统中，认为各种客观状态不是一成不变的，而是从一种状态到另一种状态不断变化的，不同时期状态转变的可能性可以用概率描述，称作状态转移矩阵，状态转移矩阵描述了系统从一个状态到另一个状态转移的百分比，这种状态转移矩阵不需要依据大量历史数据进行分析推导，仅根据短期数据即可获得。这一系列过程的整体就被称之为马尔科夫过程。因此可以通过获取系统在不同状态之间的转移概率，从而预测某动态系统状态的变化趋势，达到预测的目的。马尔科夫过程在管理预测中有着多方面的应用，本文主要从市场占有率预测、产业结构变动预测、教学效果评估和技术人员结构变动预测四方面讨论了马尔科夫过程在管理预测中的应用。

关键词：马尔科夫过程  管理预测

 

 

1．什么是马尔科夫过程

马尔可夫过程于1870 年由俄国有机化学家Markov首先予以关注，是他首先提出了马尔科夫模型并对其进行研究，又在1906 年发表了《大数定律关于相依变量的扩展》，从而为1907 年提出马尔科夫过程奠定了理论基础。1951 年日本学者伊藤清（1915-2008，日本数学家，日本学士院院士，著有《随机过程论》（1942年）和《随机过程》（1957年）等重要著作）建立了随机微分方程理论（著有《论随机微分方程》（1953年））。1954 年W．弗勒在对马尔科夫过程的研究中引入了泛函分析中的半群方法，进一步丰富了关于马尔科夫过程的研究。我国国内的研究主要起始于50 年代后期，代表人物王梓坤院士为此作出了突出贡献，他先后发表了大量著作和论文，并且翻译了国外关于马尔科夫理论的相关专著，使得这方面的研究获得了突破性的进展。

马尔科夫预测模型用数学可以描述为: 

 

    状态转移矩阵还具有一个非常重要的特性就是，经过若干时期的转移以后，系统的状态会稳定在某一个状态上保持不变，这在数学上称作马尔科夫过程的遍历性。即假定 n=3，在k→∞时，有：

 

    在应用中需要注意的是，由于实际应用中常常可能会出现转移矩阵中包含0元素，马尔科夫遍历性要求转移矩阵的主对角线上两侧的元素都必须是大于0的，满足这一条件的马尔科夫过程才具有遍历性，才有极限分布。

 

2．市场占有率预测

先看一个案例，权且记为案例一。

已知某商品在某地区的销售市场被A、B、C三个品牌占有，某一年第一季度各自的市场占有率分别为40%、30%和30%。根据市场调查，上一季度购买A品牌的顾客本季度将按照40%、30%和30%的百分比分别转向A、B、C三个品牌，上一季度购买B品牌的顾客本季度将按照60%、30%和10%的百分比分别转向A、B、C三个品牌，上一季度购买C品牌的顾客本季度也将按照60%、10%和30%的百分比分别转向A、B、C三个品牌。假定本商品的销售状态满足齐次马尔科夫过程，试问：

（1）三个季度以后，即年末的时候A、B、C三个品牌在该地区的市场占有率会是什么结果？

（2）如果顾客流向长期如此不变，A、B、C三个品牌再该地区最终的市场占有率又是什么结果？

这里已知三个品牌的初始状态为：P(0)=(0.4  0.3  0.3)

 一步转移矩阵为：

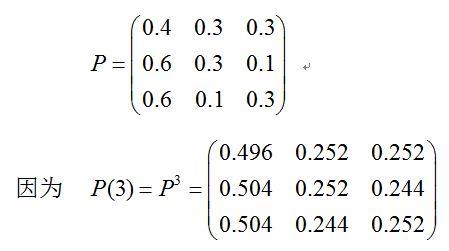
所以，3个季度后即到了年末，A、B、C三个品牌在该地区的市场占有率将变为：

解之，得到：(x₁,x₂,x₃)=(0.5,0.25,0.25)

（转移矩阵转置后特征值为1的特征向量是（0.816,0.408，0.408））

即如果顾客流动长此下去，A、B、C三个品牌的市场占有率将分别稳定在50%、25%和25%的份额上。

 

3．产业结构升级

在市场经济条件下，一个重要的市场法则，就是等量资本必须要获得等量利润。如果资本在某个产业得不到等量的利润，那么，在利益驱动下它就必然会转移到利润高的产业。同样，就劳动力而言，“人向高处走，水往低处流”是一条自然法则。随着劳动力市场的建立与不断完善，劳动力也会从劳动报酬低的产业转移到劳动报酬高的产业。资本和劳动力的不断转移，必然使得产业结构不断地得到优化和升级。

我们假定，已知某地区2010年资本和劳动力在三次产业中的分布分别为：

 

   

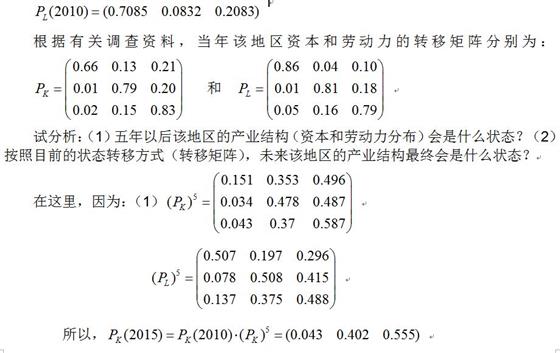
    由预测结果不难看出，资本结构5年后的状态与稳定状态已经很接近，而劳动力的结构5年后的状态与稳定状态仍然有较大差距。就劳动力的稳定状态看，与西方发达国家相比，第一产业劳动力的比重相对仍然偏大，第三产业劳动力的比重相对偏小。所以，未来该地区仍然需要加大产业结构调整的力度，以促进产业结构不断得到优化和升级。

4．教学效果评估

我们来看案例三。

    设A、B两位教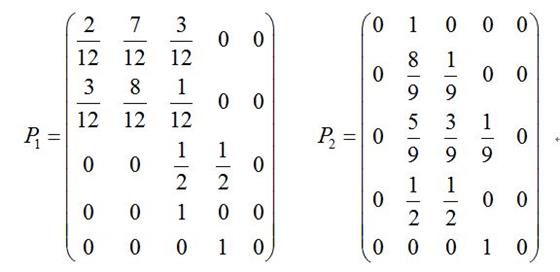师分别教授甲、乙两个班的高等数学课，A上学期和本学期都在甲班任课，B是本学期才接替另一位教师担任乙班的高等数学任课教师，两个班两学期高等数学的考试平均成绩分别是：甲班（86.61,82.29），乙班（80.78,80.33），依平均成绩看，似乎甲班比乙班要好，但是实际上如果从动态角度看结论可能会完全不同。所谓动态角度，就是说必须从两个学期中每个学生成绩的变化情况看。两个班的总人数分别为28人和27人，上学期两个班考试成绩的优异（90及以上）、良好（80-89）、中等（70-79）、及格（60-69）、不及格（60以下）的分布分别为：甲班（0.429,0.429,0.071，0.036,0.036），乙班（0.222,0.333,0.333,0.074,0.037）。经过统计分析，本学期两个班考试后的转移矩阵分别为：

试分析A、B两位老师究竟谁的教学效果更好。

在这里，本学期五个不同等级成绩的分布无需使用马氏预测方法计算，根据实际考试的结果可以使用统计方法得到。重要的问题是，按照现有的转移方式（转移矩阵），最终会稳定在一个什么样的结构上。

经计算得知，转移矩阵P₁转置后特征值为1的特征向量是（0,0,0.894,0.447,0），所以，归一化后得知，x₃=2/3，x₄=1/3。

转移矩阵P₂转置后特征值为1的特征向量是（0,0.984,0.179,0.02,0），所以，得知，x₂=0.832，x₃=0.151，x₄=,0.017。

 

取五个不同等级的中位数，即85、75和65，计算两个班稳定后的加权平均数，结果得到，即按照两个班目前的变化趋势，最终甲班的平均成绩是71.67，乙班的平均成绩是83.15，显然乙班比甲班的效果要好。

由以上分析不难看出，教学效果的评估，实际上与学生成绩的最初分布没有关系，只与状态转移方程有关。

5．技术人员结构预测

下面讨论案例四。

    根据调查和统计分析，已知2010年某公司技术人员相对于上一年的转移矩阵如下面的矩阵P所示，已知该公司2010年技术人员的结构状况是：P（2010）=（技术员，助工，工程师，总工，离退人员）=（0.2,0.3,0.25,0.15,0.1），试分析：（1）5年后该公司的技术人员结构会是什么样（注意，离退人员包括 离开公司的和退休人员）？（2）该公司最终的技术人员结构会稳定在什么结构状态上？

 

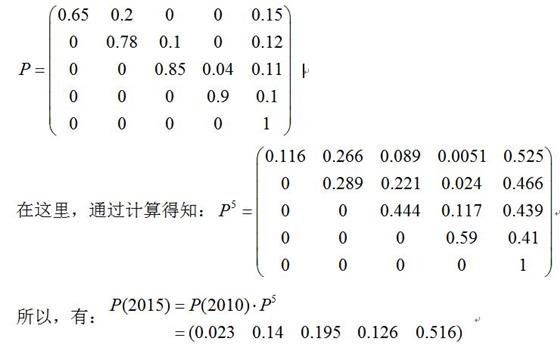
    容易看出，5年后有超过一半的技术人员都将成为离退人员。由于离退人员太多，因此在岗的前四类人员比例均下降幅度较大。因此，该公司迫切需要调整人才政策，减少技术人员跳槽，同时要积极鼓励培养技术人员，增加技术人员的后备力量。因为根据年龄，技术员和助工中的离退人员大多都属于跳槽离开公司的，工程师中离退的少量的属于跳槽离开的，总工离退的则基本上属于退休人员。

尤其重要的是，转移矩阵P转置后特征值为1的特征向量即极限分布是（0,0,0,0.,1），即按照目前的转移方式（转移矩阵），若干年后该公司的全部技术人员都将离退，公司的技术人员将归零。出现这种去矿的原因是，转移矩阵的主对角线以下的元素均为0。即公司的技术人员管理中，只能上不能下。改变这种状态的方法是，必须建立一种机制，使得技术人员能上能下，表现好的成就突出的不断晋升；表现一般成绩平平或者多年不出成果的就降级。按照目前的方式，很显然如果目前的技术人员流动状况不改变，公司就面临着崩溃和倒闭的可能。