1.1 模拟的起源和进展

人类在认识世界和改造世界的长期过程中，逐渐地认识到，在研究一个系统的时候，可以利用实物去构造一个与实际系统成比例的物理模型，然后利用物理模型去描述所研究的系统。最早的和相对简单的模拟就是物理模拟，例如人们设计的分子物理模型、天体系统模型、工程模型，典型的例子是用沙盘来模拟作战的过程，从而为制定作战计划和方案提供支持。后来发展到了电子模拟，用电子装置来模拟现实的系统，例如电子秤、电子表等。再后来发展到了工程过程模拟，例如交通系统模拟、航空航天过程模拟、军事作战等领域的模拟。近年来，模拟应用的领域发展到了管理、经济、股市、政策、虚拟世界、人工智能等领域。模拟的对象越来越复杂，模拟的过程也越来越多样化，模拟的工具也在不断地发展和完善。

实际上，人类关于模拟的思想在历史上很早就有了。例如，中国象棋其实就是对古战场的一种模拟，如炮打隔山，马踏八方，车横冲直撞，兵步步为营，士相守中宫，将帅不离宫，实际上就是古战场在棋盘上的再现。中国象棋的起源一种说法在战国时期已有了雏形，到宋时基本定型。棋语有云“棋如人生”，凡喜好中国象棋的人，无非是要论个输赢，从中获得战胜对手的乐趣。因此，凡弈棋者必然要研究胜战之策。而所有的这些胜战之策，无一不是对人类斗智斗勇谋略的“模拟”。

毫无疑问，模拟作为一种科学决策方法的提出和发展，与现代计算机科学的发展密切相关。然而这一方法建立的思路，却与一位法国科学家(原名Georges Louis Leclerc，因为在系统仿真方面的突出贡献而被封为Buffon伯爵)在200多年前提出的一个问题即蒲丰（Buffon）投针问题(1777)密切相关。问题是这样的：在平面上画一些平行线，相互间的距离都等于a，向此平面任投一长度为l 的针（ l <a）,问针与任一平行线相交的概率是多少。

    设以x表示针的中点到最近一条平行线的距离，φ表示针与平行线的交角，针与平行线的位置如图1所示，显然只有在条件： 0≤x≤a/2，0≤φ≤π，x≤(l/2)sinφ    满足时，针才与平行线相交。所以，相交的概率应该是：

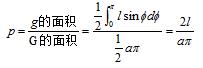
由于最后的答案与π有关，所以不少人曾经利用它来计算π的数值。方法是记下投针的次数N和相交的次数n，再代入下面的公式中计算π：

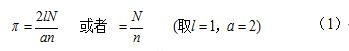
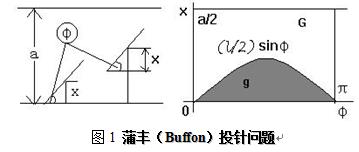
表1是投针试验的一些历史资料。

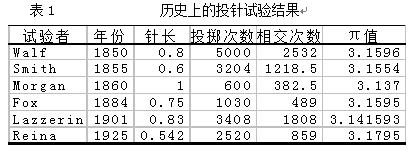上面的数学式（1）是用求定积分的方法得到的，如果你不懂积分也不要紧，下面我们用一个简单而巧妙的方法来证明它。找一根铁丝弯成一个圆圈，使其直径恰好等于平行线间的距离a。可以想象得到，对于这样的圆圈来说，不管怎么扔下，都将和平行线有两个交点。因此，如果圆圈扔下的次数为N次，那么相交的交点总数必为2N。现在设想把圆圈拉直，使其变成一条长度为a的长针。显然，这个长针扔下时（注意必须垂直扔下）与平行线相交的情形要比圆圈复杂一些，可能有4个交点，也可能是3个交点，或者2个交点，或者1个交点，甚至可能都不相交。由于这五种情况出现的机会是均等的，因此根据机会均等的原理，在投掷多次以后，它们的期望值也就是这五个数的简单平均数，即（0+1+2+3+4）/5=2。也就是说，当圆圈和长针被投掷的次数较多且相等时，两者与平行线组交点的总数可望也是一样的。这就是说，当长度为a的长针被扔下N次时，与平行线相交的交点总数应大致上也应为2N。现在转而讨论长针长度为L的情形。当投掷次数N增大的时候，这个长针跟平行线相交的交点总数n应当与长度L成正比。换句话说，当L比a更长时，相交的次数应该多于2N次，当L比a更短时，相交的次数应该少于2N次，因此，就不难建立一个比例关系式：

蒲丰问题给我们的重要启示是：可以建立一个概率模型，它与我们感兴趣的量有关（如其中的π），然后设计适当地随机试验，并通过这一试验的结果来确定这一量值（如上述的π）。现在，随着现代电子计算机的发展，人们已经按照这一思路建立了一种全新的方法，即蒙特卡罗方法（Monte-Carlo Method），也就是模拟方法或系统仿真方法。这种方法之所以被称作蒙特卡罗方法，不是没有原因的，它与蒙特卡罗这个地名密切相关。Monte Carlo是位于摩洛哥国家的一座城市，是世界著名的三大赌城之一，另两个世界级赌城一个是美国的超级赌城拉斯维加斯，另一个就是号称东方拉斯维加斯的中国澳门。蒙特卡罗概念的首次使用，起源于美国２０世纪４０年代美国的“曼哈顿工程计划”。

蒙持卡罗模拟的实质是利用服从某种分布的随机数来模拟现实系统中可能出现的随机现象, 从而为人们进行决策提供依据。由于每次模拟试验只能描述所考察系统可能出现的一次情况，只有在进行了大量次数的模拟试验后，才能根据概率论中心极限定理和大数定理，得出有价值的统计结论。由于计算机的发展，蒙持卡罗模拟目前已成为一种实用有效的决策分析方法。

    蒲丰投针问题在计算机上很容易实现[1]。

在计算机上进行模拟，必须借助于专用的计算机语言。目前，在离散系统的计算机模拟领域中，广泛使用、最为常见的语言之一就是GPSS (General Purpose Simulation System)，即通用模拟系统语言。它是一种面向过程的语言，具有很强的实用性和操作性，学习和使用起来比较方便快捷。GPSS语言是随着计算机技术的进步逐步发展起来的。1961年，IBM公司发表第一个GPSS文本，1965年又公布了GPSSIII以及扩展的C，后来相继推出了GPSSV、GPSS66、GPSS/1100等系列，还有目前广泛使用的GPSS/PC。GPSS/PC系统较为小巧，用于PC机上，使用起来很方便，每个读者都可以拥有自己的系统，在任何一台计算机上都可以运行，也给读者学习、实验提供了便利。各个不同版本的原理是一样的，如果你掌握了GPSS/PC的程序编制和使用，在别的计算机系统上也就基本上可以使用GPSS的其他版本了。新的模拟软件还包括Extend、 Agentbuild，Swarm等。

虽然计算机模拟的语言已经很丰富，然而，这些软件的使用都需要一些专门的计算机编程知识，对于学习或从事经济管理的人来说，编程技术首先就是一个“门槛”。因此，本书要介绍的是如何利用Excel来进行管理系统的计算机模拟。Excel是计算机装机必备的一个自动化办公软件，只要用电脑必不可少都会用到Excel。利用Excel进行模拟，只要掌握了模拟过程中的一些常用函数的使用，你就可以随心所欲。所以，利用Excel进行管理系统的模拟，必然将具有广阔的应用前景。

尤其是经过近十几年计算机软硬件技术的飞速发展，Excel软件目前已成为大众首选的决策分析工具软件。在它的帮助下管理人员完全可以根据实际问题，在相应的理论基础上自己动手建立计算模型并对这些模型进行各种深入的分析，特别是对于蒙特卡罗模拟这类需要建立在一定模型基础上进行分析的方法来说，Excel在建模和数据分析等方面的优势更是得到了充分的体现和发挥：

第一，Excel具有十分强大的数据分析功能，并且与各种数据库具有良好的接口，这使得操作者可以通过简单的数据分析功能直接进行一些复杂的计算和统计工作等。

第二，Excel具有大量内建函数，操作者可以利用Excel提供的各种函数公式通过确定参数的数值按特定的顺序或结构自动执行复杂的计算，可大大简化计算模型建立的过程，并有助于提高模型的准确性，特别是Excel的财务函数、统计函数等对于财务分析相关模型的建立有很大的帮助。

第三，ExceI还具有良好的图形显示功能，将这种功能与其他功能相结合，决策者可以在决策模型的基础上，经过简单的操作制作高质量的动态图形将抽象的决策模型与直观生动的图形完美结合，从而以最有效的方法帮助决策者进行各种必要的决策分析。

尤其最重要的是，利用Excel运用简单的几个函数对随机现象进行模拟，纯属于一种创新活动。有时候要运用几个函数对某个现象进行模拟，看似完全不可能，然而当你有了新的思路并按照这一思路成功地实现了对这一问题的模拟以后，你将会感到无比的自豪和兴奋，你将久久地沉浸在一种创造的乐趣之中。

END