（接续《交易的数学描述·下》）

把类似的方法用来分析所有交易者针对a、b两种商品之间的交易（包括同一件商品的反复交易）。把a、b两种商品之间的所有的交易总和起来分析，分别用Q_a和Q_b表示，就是两种商品各自的总成交量，即：

Q_a=⊿Q_a1+⊿Q_a2+⊿Q_a3+……+⊿Q_ai+……⊿Q_an=∑⊿Q_ai（i=1、2、3……n）

Q_b=⊿Q_b1+⊿Q_b2+⊿Q_b3+……+⊿Q_bi+……⊿Q_bn=∑⊿Q_bi（i=1、2、3……n）

用Q_a、Q_b构建一个平面直角坐标，例如Q_a作为横坐标，Q_b作为纵坐标（请注意：在Q_a和Q_b之间没有任何因果逻辑关系，随便哪一个都可以当作自变量，不会发生像西方微观经济学当中按照P-Q坐标可以得出价格随需求量上升而下降的结论）。用它记录持续记录所有的交易，就形成一条关于a、b两种商品的交易的“交易历史曲线”。

⊿Q_ai（⊿Q_bi）是双下标变量，也就是说，在谈论某笔交易的成交量的时候，一是要指出是那种商品的成交量，同时要指出是哪一次交易的成交量。

下图是这条“交易历史记录曲线”当中由三笔交易构成的一段：

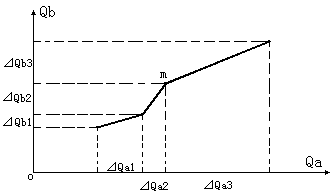
任意第i次交易的价格Pi=⊿Qai /⊿Qbi。

请注意：⊿Q_a/⊿Q_b是价格的定义式，即P≡⊿Q_a/⊿Q_b（或用倒数表示），即在价格P和交易量⊿Q_a、⊿Q_b之间具有人为赋予的因果逻辑关系，等式左边的价格是“果”，右边的⊿Q_a、⊿Q_b是“因”。但是两个因之间并没有任何关系。用平面坐标的表述也不代表两者之间有任何逻辑关系。

显然，Pi就是表示第i次交易的那段直线的斜率。

以上方法也可以用于某商品的单一供给者的销售，例如某市场某商品的销售分析。

 

在Q_a=∑⊿Q_ai、Q_b=∑⊿Q_bi当中，⊿Q_ai、⊿Q_bi是发生在一个具体时点上的交易量，是交易双方各自最终摆在台面上用于交易的两种商品的量，是时点数，即存量。注意，这里的“存量”所指的时点，是两种商品所有权的互易成立的时点。所有权变更是同时在某个时点上生效的。

而Q_a、Q_b是截止到当前第n次交易的总交易量。作为各个存量（⊿Q_i）的和，Q_a、Q_b当然也是存量，即时点数，对应于当前的、最后一次交易的时点。i表示交易的先后顺序，i=1、2、3……即第一笔、第二笔……。

由于交易量恒为正值，所以这条折线是逐步向上的，即单调递增。颠倒纵横坐标并不改变这种单调递增的性质，即Q_a随Q_b的增加而增加，或者Q_b随Q_a的增加而增加。这种单调递增的性质，就是《西方经济学的终结》用“水表数”这种形象的说法表示这种性质，即“流存量”性质。

反过来，如果为了研究某次交易，只需要研究这个单调递增折线当中的一段即可。在一段（一次交易）当中，Q_a=⊿Q_ai，Q_b=⊿Q_bi。

根据总平均价格的定义（两个总交易量的比值）可知，从任何一个节点（如上图中的m点）到原点的连线的斜率，就是这个节点之前的所有交易的平均价格。

作为经济学研究量价关系，一定要指出所谓的“价”是具体某笔交易（甲和乙交换a和b）的交换比例，还是累积的“平均价格”；当提到“需求量”“购买量”的时候也一定要指出是⊿Q_i，还是Q_i，抑或是某一指定时段内的累积交易量，当然还要指出是针对a商品的，还是针对b商品的。

传统的经济学把一大堆概念笼统地称为“价格”或“需求量”，连张三李四都分不清楚。不知道价格为何物，谈“需求量”也不知道其确切的统计方法，自然无法得到任何正确的结论。

 

为了能够更好的研究大宗的、连续的、经常的交易，可以把这条单调递增的折线简单化地当做是一条平滑的曲线（即把坐标刻度密度任意加大）。则这条曲线（图中粗线）上任意一点的斜率，就表示a、b两种商品当时的那笔交易的价格。

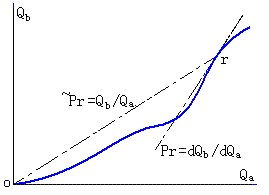
此时的价格定义具有更一般的数学表达形式，即 P≡dQ_b/dQ_a

这种研究思路适合于任何“商品对”之间的交换。

 

如果商品b是货币，则交换形态就是我们日常所熟悉的“用货币购物”的情况，即货币经济形态。“以币购物”不过是一个特例的交换形式。此时，习惯上把Qb当作是销售a货物的甲方的“销售收入”或“总收益TR”。则上述价格的一般表述就变成了：

P≡MR

也就是说，瞬时的价格就是最近一笔交易的“边际收益MR”。也就是交易历史记录曲线上的某点r的切线的斜率。

MR≡dTR/dQ_a，即边际收益（MR）恒等于最近价格（P）。这就是MR的定义式。不存在微观经济学所称的有时“等于”，有时“不等于”的情况。dTR/dQ_a这种表述，非常准确地表达了“最后一个销售单位的收益”的概念，也就是最后一次交易的单价。现实当中任何商品（包括货币）都有最小单位，但这并不影响用微分极限的概念去从理论上进行分析。

此时，总收益TR与总销售量Qa的比值，就代表截止到当前为止的所有交易的平均价格。也就是在曲线上任何一点到原点的连接线的斜率（~Pr）。

 

由于在同一个交易合约当中只能有一个价格（或者说把按照同一个价格成交的当作一次交易），所以，对于一笔交易来说，从价格的定义式P=TR/Q来说，可以反过来用销量Q乘以合同价格P来计算TR，即TR=PQ。

这种计算当中有两个不当之处。第一，纯属数字计算。因为TR是可以直接测度的基础数据，而P是结果，不需要反过来计算它。老板只需要直接问一下收银员钱柜里的钞票数就行了。第二，这种计算只使用于按照固定比例（价格）进行的交易，在此P是常数，而不是一个变量，反过来要把P当作变量，则不能用P·Q计算收益，只能用dTR/dQ_a求价格。

此时用瞬时价格计算总收益的方法是积分：TR=∫PdQ。

需要指出的是，用微分方法求价格仅仅是一种理论分析思路，对于现实的经济，重要的、有用的是当前交易的价格，这不需要用到什么高深的数学方法，得知交易点坐标（⊿Q_a，⊿Q_b），也就得到了关于此次交易的基本信息。

 

本文的分析方法具有普适性，适用于任何两种商品之间的交换，包括易物交换、货币购物、票证交易以及汇市上的币币交易等等。（全文完）